Table of Contents
In the world of computer science and digital technology, numbers are not just abstract concepts but form the backbone of how data is represented and processed. From counting objects to powering the complex operations within a computer, understanding different number systems is key to unlocking the secrets of digital systems. This guide explores the essential number systems—Decimal, Binary, Octal, and Hexadecimal—and dives deeper into how computers rely on the binary number system for everything they do, from arithmetic to data storage.
What is Number System?
A number system is a way of representing and expressing numbers using a set of symbols and rules. It defines how numbers are written and interpreted in different forms, allowing us to perform mathematical calculations, store data, and communicate values. The most commonly used number system in everyday life is the decimal system (Base-10), which uses ten digits (0-9). However, in computing, other number systems like binary number system (Base-2), octal (Base-8), and hexadecimal (Base-16) are widely used.
Types of Number System
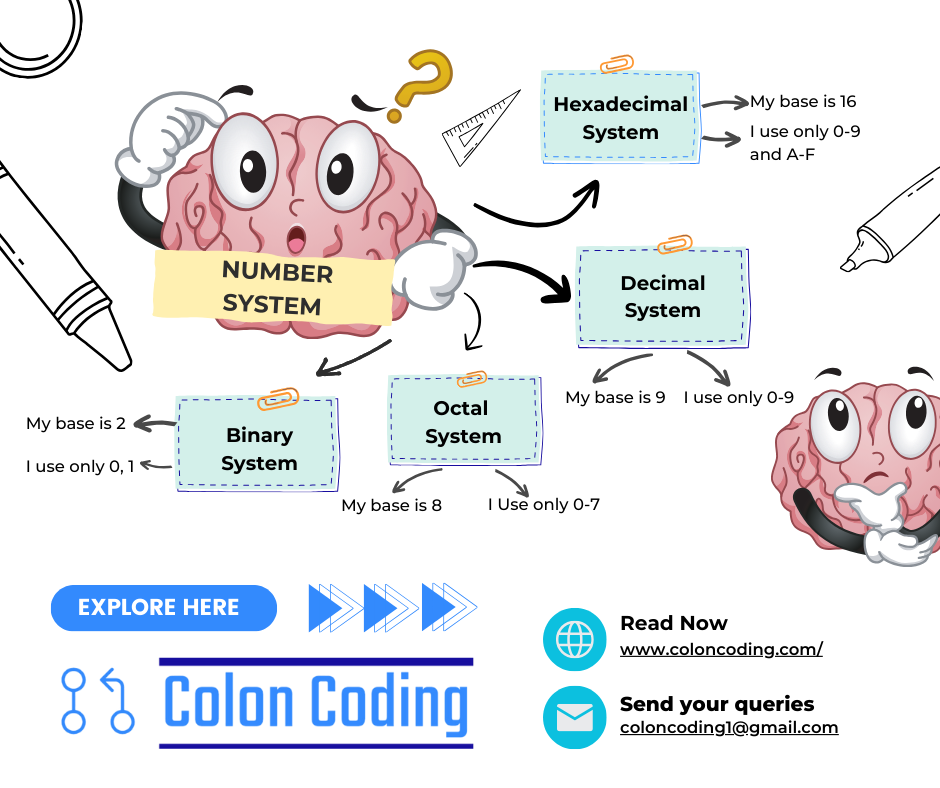
In computer science, several number systems are used to represent data including binary number system, each with its own base and practical applications. Let’s take a closer look at each of these number systems:
| Number System | Overview | Example |
| Decimal (Base-10) | The most widely used system in everyday life, consisting of ten digits (0-9). Each position in a decimal number represents a power of 10. | 123 (Decimal) = 1 * 102 + 2 * 101 + 3 * 100 = 123 |
| Binary Number System (Base-2) | The most fundamental system in computing, using only two digits (0 and 1). Each position represents a power of 2. | 1011 (Binary) = 1 * 23 + 0 * 22 + 1 * 21 + 1 * 20 = 11 (Decimal) |
| Octal (Base-8) | The octal system uses eight digits (0-7) and was historically used in early computing. | 12 (Octal) = 1 * 81 + 2 * 80 = 10 (Decimal) |
| Hexadecimal (Base-16) | Uses sixteen symbols (0-9 and A-F) and is widely used in computing for memory addressing. | 1A (Hexadecimal) = 1 * 161 + A * 160 = 26 (Decimal) |
Binary Number System in Computers
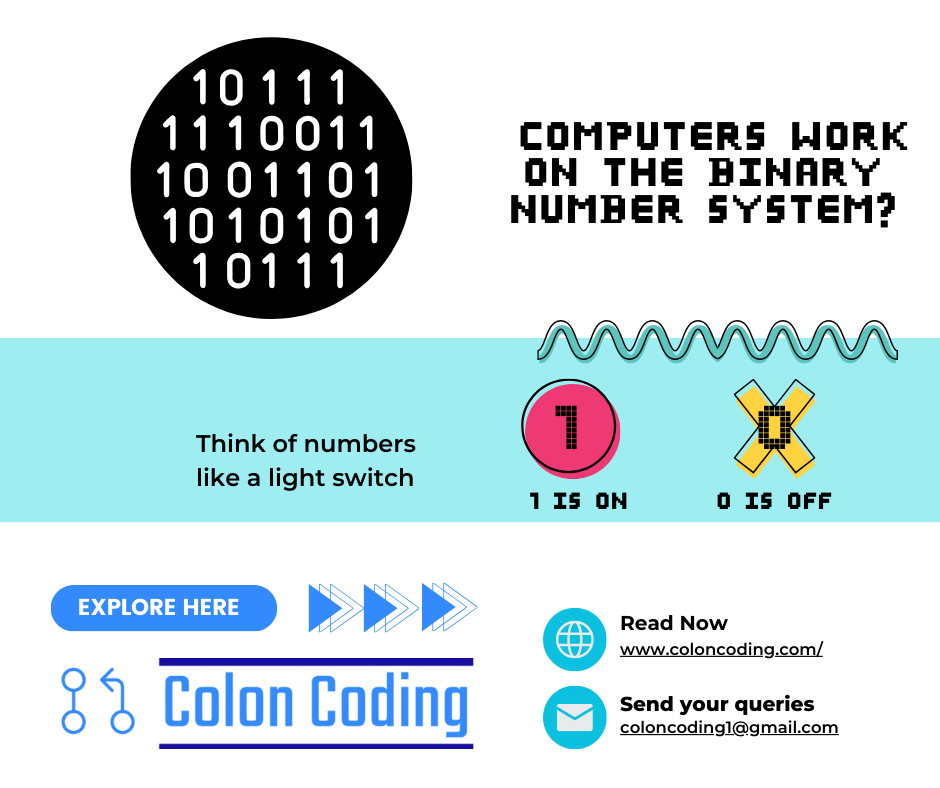
The binary number system (Base-2) plays a central role in computing because it aligns with the physical nature of computer hardware. Computers operate on two states—on and off—which correspond to the binary digits 1 and 0, making binary the perfect system for digital operations.
Binary Numbers as the Language of Computers
Computers represent all forms of data—whether numbers, text, or instructions—in binary. For instance, the letter ‘A’ in the ASCII encoding system is represented as 01000001 in binary, corresponding to its decimal ASCII value of 65.
Memory and Storage in Binary Number System
In computer memory, data is stored in binary form, typically organized into bytes (groups of 8 bits). Each byte can represent 256 different values, ranging from 00000000 (0 in decimal) to 11111111 (255 in decimal). The combination of bits and bytes allows computers to represent and process a wide range of data, from simple numbers to complex multimedia files.
For example consider a 4-byte memory block storing the number 145 in binary: The binary representation of 145 is 10010001. In this case, the computer uses 1 byte (8 bits) to store the value of 145. This works because 1 byte can store numbers from 0 to 255 (which includes 145).
Data Representations in Binary Number System
- Text and Characters: Text is represented in binary number system through encoding schemes like ASCII or Unicode. Each character is assigned a unique binary code. For example the character ‘B’ has an ASCII value of 66, represented as 01000010 in binary.
- Numbers: Computers store both integers and floating-point numbers in binary number system. For integers, the representation is straightforward, while floating-point numbers involve a more complex format.
- Images: Images are composed of tiny elements called pixels, where each pixel represents a specific color. Computers represent each of these colors in binary. The most common color model is RGB (Red, Green, Blue), where each color is broken down into varying levels of red, green, and blue values. For instance, a pixel in an image might have an RGB value of (255, 0, 0), which represents a bright red color. Each of these color values is stored in binary: Red: 255 → 11111111, Green: 0 → 00000000, Blue: 0 → 00000000. Thus, the binary representation of this red pixel would be 11111111 00000000 00000000.
- Audio data: Audio data is stored as a series of binary numbers that represent sound waves. These sound waves are converted into digital signals through a process called sampling, where the amplitude (loudness) of the sound wave is recorded at regular intervals.
- Video: Video is essentially a series of images (frames) played rapidly to create motion. Each frame is stored as an image in binary, similar to how still images are stored. Videos also contain audio, which is stored as described above.
Conclusion
Understanding the number systems used in computing, particularly the binary system, is essential for anyone delving into computer science and programming or digital technology. From representing text and numbers to performing arithmetic operations and building digital circuits, binary is at the core of how computers function. A solid grasp of binary and other number systems helps demystify the inner workings of computers and opens the door to more advanced topics in computing.
FAQs
Why do computers use the binary system instead of the decimal system?
Computers use the binary system because it aligns with their hardware, which operates on two states: on (1) and off (0). Binary is the simplest and most efficient way for computers to process data.
What is the difference between binary and decimal arithmetic?
Binary arithmetic uses only two digits (0 and 1), whereas decimal arithmetic uses ten digits (0-9). The rules of arithmetic are similar, but binary operations are simpler and faster for computers to perform.
Can humans easily work with binary numbers?
While humans typically use the decimal system, binary is not as intuitive due to its large number of digits. However, tools and calculators make working with binary easier for specific applications like computing.
How does hexadecimal relate to binary?
Hexadecimal (Base-16) is often used in computing because it’s more compact than binary. Each hexadecimal digit represents four binary digits (bits), making it easier to read and manage large binary numbers.







